Virtually everyone has had an online experience where a website makes personalized recommendations in hopes of futurity sales or ongoing traffic. Amazon tells you "Customers Who Bought This Item Also Bought", Udemy tells you "Students Who Viewed This Grade Also Viewed". And Netflix awarded a $1 million prize to a programmer team in 2009, for an algorithm that increased the accurateness of the visitor'southward recommendation system past x percent.

Without further ado, if yous want to learn how to build a recommender organisation from scratch, let's become started.

The Information

Book-Crossings is a book rating dataset compiled by Cai-Nicolas Ziegler. It contains 1.1 million ratings of 270,000 books by 90,000 users. The ratings are on a scale from 1 to 10.

The data consists of three tables: ratings, books info, and users info. I downloaded these three tables from here.

import pandas equally pd import numpy as np import matplotlib.pyplot every bit plt books = pd.read_csv('BX-Books.csv', sep=';', error_bad_lines=False, encoding="latin-1") books.columns = ['ISBN', 'bookTitle', 'bookAuthor', 'yearOfPublication', 'publisher', 'imageUrlS', 'imageUrlM', 'imageUrlL'] users = pd.read_csv('BX-Users.csv', sep=';', error_bad_lines=False, encoding="latin-1") users.columns = ['userID', 'Location', 'Age'] ratings = pd.read_csv('BX-Book-Ratings.csv', sep=';', error_bad_lines=False, encoding="latin-1") ratings.columns = ['userID', 'ISBN', 'bookRating']

Ratings data

The ratings information set provides a list of ratings that users take given to books. It includes 1,149,780 records and 3 fields: userID, ISBN, and bookRating.

impress(ratings.shape) impress(list(ratings.columns))            (1149780, 3) ['userID', 'ISBN', 'bookRating']

Ratings distribution

The ratings are very unevenly distributed, and the vast bulk of ratings are 0.

plt.rc("font", size=15) ratings.bookRating.value_counts(sort=False).plot(kind='bar') plt.championship('Rating Distribution\n') plt.xlabel('Rating') plt.ylabel('Count') plt.savefig('system1.png', bbox_inches='tight') plt.prove()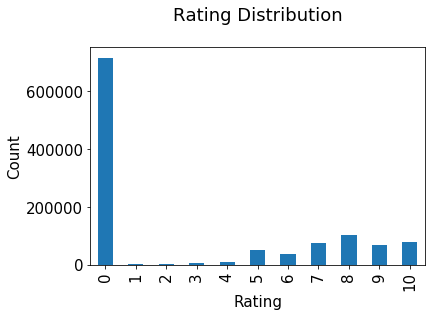

Books data

The books dataset provides book details. It includes 271,360 records and 8 fields: ISBN, volume title, book author, publisher and so on.

impress(books.shape) impress(listing(books.columns))            (271360, viii) ['ISBN', 'bookTitle', 'bookAuthor', 'yearOfPublication', 'publisher', 'imageUrlS', 'imageUrlM', 'imageUrlL']

Users data

This dataset provides the user demographic information. Information technology includes 278,858 records and iii fields: user id, location, and historic period.

print(users.shape) impress(list(users.columns))            (278858, 3) ['userID', 'Location', 'Age']

Age distribution

The almost active users are amidst those in their 20–30s.

users.Historic period.hist(bins=[0, 10, twenty, 30, 40, 50, 100]) plt.title('Historic period Distribution\northward') plt.xlabel('Historic period') plt.ylabel('Count') plt.savefig('system2.png', bbox_inches='tight') plt.show()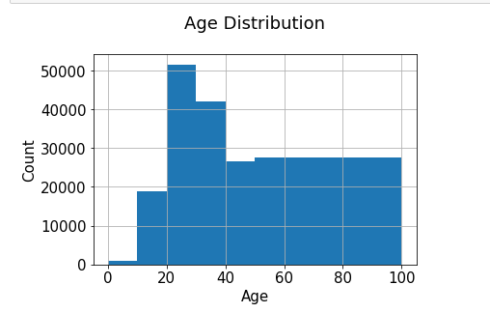

Recommendations based on rating counts

rating_count = pd.DataFrame(ratings.groupby('ISBN')['bookRating'].count()) rating_count.sort_values('bookRating', ascending=False).head()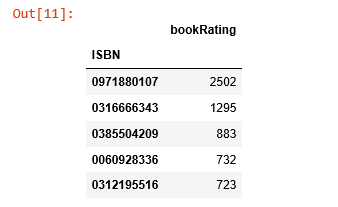

The book with ISBN "0971880107" received the about rating counts. Allow's discover out what book it is, and what books are in the top 5.

most_rated_books = pd.DataFrame(['0971880107', '0316666343', '0385504209', '0060928336', '0312195516'], alphabetize=np.arange(5), columns = ['ISBN']) most_rated_books_summary = pd.merge(most_rated_books, books, on='ISBN') most_rated_books_summary

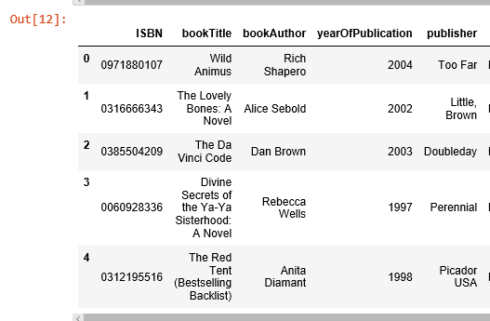
The book that received the most rating counts in this data set is Rich Shapero's "Wild Animus". And there is something in common amongst these five books that received the about rating counts — they are all novels. The recommender suggests that novels are popular and likely receive more ratings. And if someone likes "The Lovely Basic: A Novel", we should probably also recommend to him(or her) "Wild Animus".

Recommendations based on correlations

We use Pearsons'R correlation coefficient to measure the linear correlation between two variables, in our case, the ratings for two books.

First, nosotros need to observe out the boilerplate rating, and the number of ratings each book received.

average_rating = pd.DataFrame(ratings.groupby('ISBN')['bookRating'].mean()) average_rating['ratingCount'] = pd.DataFrame(ratings.groupby('ISBN')['bookRating'].count()) average_rating.sort_values('ratingCount', ascending=False).caput()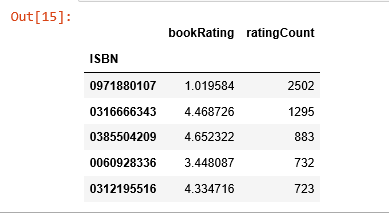

Observations: In this data set, the book that received the most rating counts was not highly rated at all. As a result, if we were to use recommendations based on rating counts, we would definitely make mistakes here. So, we need to have a better system.

To ensure statistical significance, users with less than 200 ratings, and books with less than 100 ratings are excluded.

counts1 = ratings['userID'].value_counts() ratings = ratings[ratings['userID'].isin(counts1[counts1 >= 200].index)] counts = ratings['bookRating'].value_counts() ratings = ratings[ratings['bookRating'].isin(counts[counts >= 100].index)]

Rating matrix

We convert the ratings table to a 2D matrix. The matrix will exist sparse considering not every user rated every volume.

ratings_pivot = ratings.pin(index='userID', columns='ISBN').bookRating userID = ratings_pivot.alphabetize ISBN = ratings_pivot.columns print(ratings_pivot.shape) ratings_pivot.head()            (905, 207699)

Permit'south find out which books are correlated with the second nigh rated book "The Lovely Basic: A Novel".

To quote from Wikipedia: "It is the story of a teenage girl who, after being raped and murdered, watches from her personal Heaven as her family unit and friends struggle to movement on with their lives while she comes to terms with her own decease".

bones_ratings = ratings_pivot['0316666343'] similar_to_bones = ratings_pivot.corrwith(bones_ratings) corr_bones = pd.DataFrame(similar_to_bones, columns=['pearsonR']) corr_bones.dropna(inplace=True) corr_summary = corr_bones.join(average_rating['ratingCount']) corr_summary[corr_summary['ratingCount']>=300].sort_values('pearsonR', ascending=Simulated).head(10)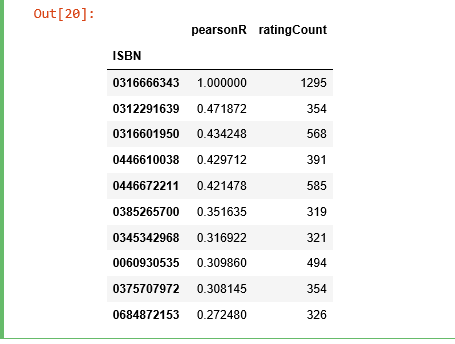

Nosotros obtained the books' ISBNs, but nosotros demand to detect out the titles of the books to run into whether they make sense.

books_corr_to_bones = pd.DataFrame(['0312291639', '0316601950', '0446610038', '0446672211', '0385265700', '0345342968', '0060930535', '0375707972', '0684872153'],                                    index=np.arange(ix), columns=['ISBN']) corr_books = pd.merge(books_corr_to_bones, books, on='ISBN') corr_books

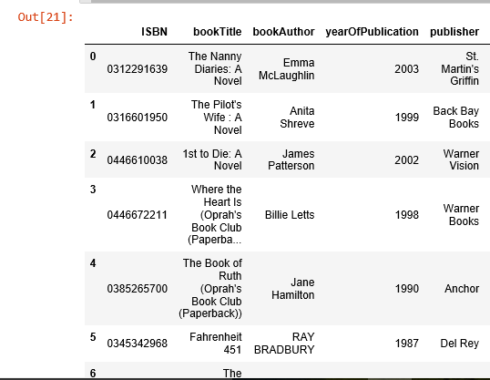
Let'southward select three books from the to a higher place highly correlated list to examine: "The Nanny Diaries: A Novel", "The Airplane pilot's Married woman: A Novel" and "Where the Heart is".

"The Nanny Diaries" satirizes upper-grade Manhattan society every bit seen through the eyes of their children's caregivers.

Written by the same writer as "The Lovely Basic", "The Pilot's Wife" is the 3rd novel in Shreve'southward informal trilogy to exist gear up in a large embankment house on the New Hampshire declension that used to be a convent.

"Where the Heart Is" dramatizes in detail the tribulations of lower-income and foster children in the Usa.

These three books sound like they would be highly correlated with "The Lovely Basic". It seems our correlation recommender arrangement is working.

Collaborative Filtering Using g-Nearest Neighbors (kNN)

kNN is a machine learning algorithm to detect clusters of similar users based on common book ratings, and brand predictions using the average rating of top-g nearest neighbors. For example, we commencement present ratings in a matrix with the matrix having 1 row for each item (book) and one cavalcade for each user, like then:

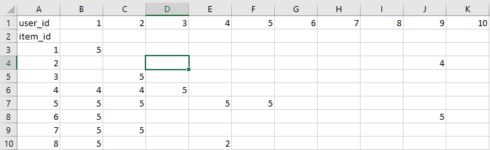
We so discover the k item that has the nearly similar user engagement vectors. In this instance, Nearest Neighbors of item id 5= [7, four, 8, …]. At present, let'south implement kNN into our book recommender system.

Starting from the original data gear up, we will be only looking at the popular books. In order to find out which books are popular, we combine books data with ratings data.

combine_book_rating = pd.merge(ratings, books, on='ISBN') columns = ['yearOfPublication', 'publisher', 'bookAuthor', 'imageUrlS', 'imageUrlM', 'imageUrlL'] combine_book_rating = combine_book_rating.drop(columns, axis=1) combine_book_rating.head()

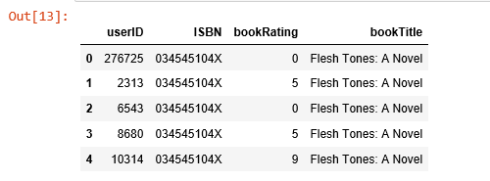
Nosotros then group by book titles and create a new cavalcade for total rating count.

combine_book_rating = combine_book_rating.dropna(axis = 0, subset = ['bookTitle'])  book_ratingCount = (combine_book_rating.      groupby(past = ['bookTitle'])['bookRating'].      count().      reset_index().      rename(columns = {'bookRating': 'totalRatingCount'})      [['bookTitle', 'totalRatingCount']]     ) book_ratingCount.head()

We combine the rating information with the total rating count data, this gives us exactly what we need to notice out which books are popular and filter out lesser-known books.

rating_with_totalRatingCount = combine_book_rating.merge(book_ratingCount, left_on = 'bookTitle', right_on = 'bookTitle', how = 'left') rating_with_totalRatingCount.caput()

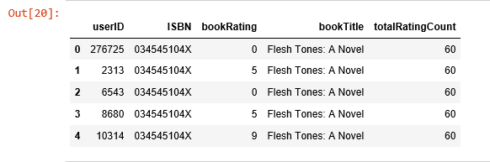
Allow'south expect at the statistics of full rating count:

pd.set_option('display.float_format', lambda x: '%.3f' % x) print(book_ratingCount['totalRatingCount'].describe())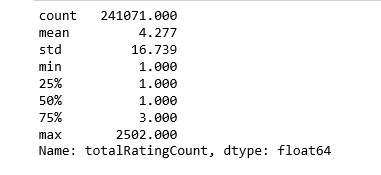

The median book has been rated simply once. Let'southward look at the top of the distribution:

impress(book_ratingCount['totalRatingCount'].quantile(np.arange(.ix, 1, .01)))

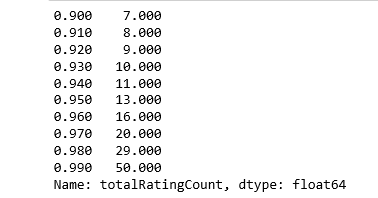
About i% of the books received 50 or more ratings. Considering we have so many books in our information, we will limit it to the acme one%, and this will requite the states 2713 unique books.

popularity_threshold = 50 rating_popular_book = rating_with_totalRatingCount.query('totalRatingCount >= @popularity_threshold') rating_popular_book.head()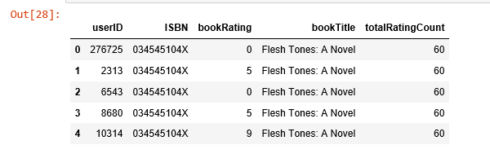

Filter to users in U.s.a. and Canada only

In guild to improve computing speed, and not see the "MemoryError" consequence, I will limit our user information to those in the The states and Canada. And so combine user data with the rating data and total rating count data.

combined = rating_popular_book.merge(users, left_on = 'userID', right_on = 'userID', how = 'left')  us_canada_user_rating = combined[combined['Location'].str.contains("us|canada")] us_canada_user_rating=us_canada_user_rating.drop('Age', axis=1) us_canada_user_rating.caput()

Implementing kNN

Nosotros catechumen our table to a 2d matrix, and make full the missing values with zeros (since nosotros will calculate distances betwixt rating vectors). We then transform the values(ratings) of the matrix dataframe into a scipy sparse matrix for more efficient calculations.

Finding the Nearest Neighbors

We use unsupervised algorithms with sklearn.neighbors. The algorithm nosotros employ to compute the nearest neighbors is "creature", and we specify "metric=cosine" so that the algorithm will summate the cosine similarity between rating vectors. Finally, nosotros fit the model.

us_canada_user_rating = us_canada_user_rating.drop_duplicates(['userID', 'bookTitle']) us_canada_user_rating_pivot = us_canada_user_rating.pivot(alphabetize = 'bookTitle', columns = 'userID', values = 'bookRating').fillna(0) us_canada_user_rating_matrix = csr_matrix(us_canada_user_rating_pivot.values)  from sklearn.neighbors import NearestNeighbors  model_knn = NearestNeighbors(metric = 'cosine', algorithm = 'brute') model_knn.fit(us_canada_user_rating_matrix)            NearestNeighbors(algorithm='animate being', leaf_size=xxx, metric='cosine',          metric_params=None, n_jobs=i, n_neighbors=5, p=two, radius=1.0)

Test our model and brand some recommendations:

In this step, the kNN algorithm measures distance to determine the "closeness" of instances. It then classifies an instance past finding its nearest neighbors, and picks the most popular class amongst the neighbors.

query_index = np.random.selection(us_canada_user_rating_pivot.shape[0]) distances, indices = model_knn.kneighbors(us_canada_user_rating_pivot.iloc[query_index, :].reshape(1, -1), n_neighbors = 6)  for i in range(0, len(distances.flatten())):     if i == 0:         impress('Recommendations for {0}:\n'.format(us_canada_user_rating_pivot.index[query_index]))     else:         impress('{0}: {i}, with distance of {2}:'.format(i, us_canada_user_rating_pivot.index[indices.flatten()[i]], distances.flatten()[i]))            Recommendations for the Green Mile: Coffey's Hands (Dark-green Mile Series):  one: The Dark-green Mile: Night Journeying (Green Mile Series), with distance of 0.26063737394209996: 2: The Green Mile: The Mouse on the Mile (Dark-green Mile Series), with distance of 0.2911623754404248: 3: The Green Mile: The Bad Death of Eduard Delacroix (Green Mile Serial), with distance of 0.2959542871302775: 4: The Two Dead Girls (Green Mile Serial), with distance of 0.30596709534565514: 5: The Green Mile: Coffey on the Mile (Green Mile Series), with distance of 0.37646848777592923:

Perfect! Light-green Mile Series books definitely should exist recommended, one after another.

Collaborative Filtering Using Matrix Factorization

Matrix Factorization is simply a mathematical tool for playing around with matrices. The Matrix Factorization techniques are usually more constructive, considering they permit users to discover the latent (subconscious)features underlying the interactions between users and items (books).

We employ atypical value decomposition (SVD) — 1 of the Matrix Factorization models for identifying latent factors.

Similar with kNN, nosotros convert our USA Canada user rating tabular array into a 2D matrix (chosen a utility matrix here) and fill the missing values with zeros.

us_canada_user_rating_pivot2 = us_canada_user_rating.pivot(index = 'userID', columns = 'bookTitle', values = 'bookRating').fillna(0) us_canada_user_rating_pivot2.head()

We then transpose this utility matrix, so that the bookTitles get rows and userIDs become columns. After using TruncatedSVD to decompose information technology, we fit it into the model for dimensionality reduction. This compression happened on the dataframe'due south columns since nosotros must preserve the book titles. Nosotros choose n_components = 12 for merely 12 latent variables, and you lot can see, our data'southward dimensions have been reduced significantly from 40017 X 2442 to 2442 X 12.

us_canada_user_rating_pivot2.shape            (40017, 2442)                      
X = us_canada_user_rating_pivot2.values.T Ten.shape            (2442, 40017)                      
import sklearn from sklearn.decomposition import TruncatedSVD  SVD = TruncatedSVD(n_components=12, random_state=17) matrix = SVD.fit_transform(Ten) matrix.shape            (2442, 12)

We calculate the Pearson's R correlation coefficient for every volume pair in our concluding matrix. To compare this with the results from kNN, nosotros selection the same volume "The Green Mile: Coffey'south Hands (Green Mile Series)" to find the books that have high correlation coefficients (between 0.nine and 1.0) with it.

import warnings warnings.filterwarnings("ignore",category =RuntimeWarning) corr = np.corrcoef(matrix) corr.shape            (2442, 2442)                      
us_canada_book_title = us_canada_user_rating_pivot2.columns us_canada_book_list = listing(us_canada_book_title) coffey_hands = us_canada_book_list.index("The Green Mile: Coffey's Hands (Green Mile Series)") impress(coffey_hands)            1906

There you accept it!

corr_coffey_hands  = corr[coffey_hands] listing(us_canada_book_title[(corr_coffey_hands0.9)])            ['Needful Things',  'The Bachman Books: Rage, the Long Walk, Roadwork, the Running Man',  'The Light-green Mile: Coffey on the Mile (Greenish Mile Series)',  'The Light-green Mile: Night Journeying (Green Mile Series)',  'The Green Mile: The Bad Decease of Eduard Delacroix (Green Mile Serial)',  'The Green Mile: The Mouse on the Mile (Green Mile Series)',  'The Shining',  'The Two Dead Girls (Green Mile Series)']

Not too shabby! Our system tin can beat Amazon'due south, what do you recall?

References:

    Music Recommendations
    ohAI